Answer: (a)
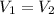 = 24.75x
= 24.75x
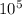 V
V
(b)
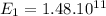 V/m
V/m
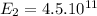 V/m
V/m
Explanation: Eletric Potential (V) is the amount of energy necessary to move a charged particle inside an electric field. It is calculated as:
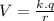
where:
k is coulomb's constant: k = 9.
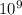 N.m²/C²
N.m²/C²
q is the charge of the object
r is the distance
Electric Field (E) is what surrounds an electric particle in a way that every particle inside the field is influenciated by it, through force of attraction or of repulsion. When related to electric potential, can be calculated as: E =
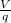
a) The ratio of the two charges is proportional to the ratio of the two radii:
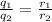
where 1 represents the sphere of the body of the airplane and 2 is the tip of the needle.
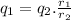
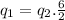
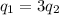 (1)
(1)
The combine charges of spheres results in a charge of 22.0µC, which means:
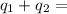 22.
22.
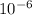
Substitute and resolve:
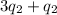 = 22.
= 22.
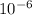
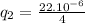
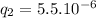 C
C
Using (1) to find the other charge:
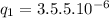
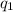 = 16.5.
= 16.5.
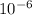 C
C
Now, to determine electric potential for each sphere:
Electric Potential for Sphere 1:
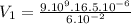
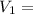 24.75.
24.75.
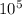 V
V
Electric Potential for Sphere 2:
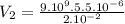
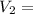 24.75.
24.75.
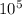 V
V
The electric potential of each sphere is the same and has magnitude 24.75.
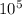 V.
V.
b) Electric Field for Sphere 1:
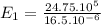
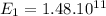 V/m
V/m
Electric field for Sphere 2:
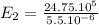
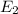 =
=
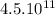 V/m
V/m