Question

A study was conducted to determine whether magnets were effective in treating pain. The values represent measurements of pain using the visual analog scale. Assume that both samples are independent simple random samples from populations having normal distributions. Use a 0.05 significance level to test the claim that those given a sham treatment have pain reductions that vary more than the pain reductions for those treated with magnets.

Sham: n=20, xÌ=0.44,s=1.24n=20, xÌ=0.44,s=1.24
Magnet: n=20, xÌ=0.49,s=0.95

Required:
a. Identify the test statistic. (Round to two decimal places as needed)
b. Use technology to identify the P-value. (Round to three decimal places as needed)
c. What is the conclusion for this hypothesis test?

Answer 1

Given:

Sham: n= 20, x=0.44, s=1.24,

Magnet:n= 20, x =0.49, s= 0.95

For Sham:

Sample size, n = 20

Sample mean = 0.44

Standard deviation = 1.24

For Magnet:

Sample size = 20

Sample mean = 0.49

Standard deviation = 0.95

The null and alternative hypotheses:

H0: s1²=s2²

H1: s1² ≠ s2²

a) To find the test statistics, use the formula:

`(s1^2)/(s2^2)`

`(1.24^2)/(0.95^2) = (1.5376)/(0.9025) = 1.7037`

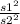
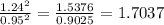
Test statistics = 1.7037

b) P-value:

Sham: degrees of freedom
`= n - 1 = 20 - 1 = 19`

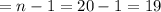
Magnet: degrees of freedom
`= n - 1 = 20 - 1 = 19`

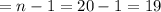
The critical values:

[Za/2, df1, df2)], [(1 - Za/2), df1, df2]

`f[0.05/2, 19, 19], f[(1 - 0.05/2), 19, 19]`

`f[0.025, 19, 19], f[0.975, 19, 19]`

`(2.526, 0.3958)`

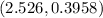
The rejection region:

Reject H0, if F < 0.3958 or if F > 2.526

c) Conclusion:

Since the critical values of test statistic is between (0.3958 < 1.7037 < 2.526), we fail to reject null hypothesis H0.

There is insufficient evidence to to support the claim that those given a sham treatment have reductions that vary more than those treated with magnets