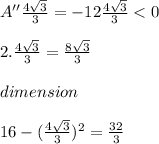Question

A rectangle is constructed with its base on the​ x-axis and two of its vertices on the parabola yequals25minusxsquared. What are the dimensions of the rectangle with the maximum​ area? What is the​ area?

Answer 1

The answer is "
`\bold{(32)/(3)}\\`"

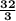Explanation:

The rectangle should also be symmetrical to it because of the symmetry to the y-axis The pole of the y-axis. Its lower two vertices are (-x,0). it means that

and (-x,0), and (x,0). Therefore the base measurement of the rectangle is 2x. The top vertices on the parabola are as follows:

The calculation of the height of the rectangle also is clearly 16-x^2, (-x,16,-x^2) and (x,16,-x^2).

The area of the rectangle:

`A(x)=(2x)(16-x^2)\\\\A(x)=32x-2x^3`

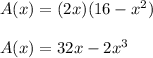
The local extremes of this function are where the first derivative is 0:

`A'(x)=32-6x^2\\\\32-6x^2=0\\\\x= \pm\sqrt{(32)/(6)}\\\\x= \pm(4√(3))/(3)\\\\`

Simply ignore the negative root because we need a positive length calculation

It wants a maximum, this we want to see if the second derivative's profit at the end is negative.

`A''(4√(3))/(3) = -12(4√(3))/(3)<0\\\\2.(4√(3))/(3)= (8√(3))/(3)\\\\\vertical \ dimension\\\\16-((4√(3))/(3))^2= (32)/(3)`