Answer:
a. SST = 1816
SSR = 1511.804
SSE = 465.804
b. Coefficient of determination, R² = 0.832491079
c. The correlation coefficient r = 0.8636
Explanation:
y = 23.194 + 0.318·x
Where:
x = Price
y = Overall score
The observed data are given as follows;
Brand Price Score
Bose 180 76
Scullcandy 150 71
Koss 95 62
Phillips/O'Neill 70 57
Denon 70 30
JVC 35 34
 = 1816
= 1816
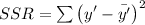 = 1511.804
= 1511.804
 = 465.804
= 465.804
Coefficient of determination
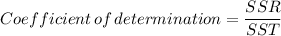 = 0.832
= 0.832
Coefficient of correlation =
![r = \frac{n\left (\sum xy \right )-\left (\sum x \right )\left (\sum y \right )}{\sqrt{\left [n\sum x^(2)-\left (\sum x \right )^(2) \right ]\left [n\sum y^(2)-\left (\sum y \right )^(2) \right ]}}](https://img.qammunity.org/2021/formulas/mathematics/college/5rfxps1es495pvq0gcf1rhlt15wor1jnsr.png)
Ʃxy = 37500
Ʃx =600
Ʃy = 330
Ʃx² = 74950
Ʃy² = 19966
![r = \frac{6 \left (37500 \right )-\left (600 \right )\left (330 \right )}{\sqrt{\left [6* 74950-\left (600 \right )^(2) \right ]\left [6 * 19966-\left (330 \right )^(2) \right ]}} = 0.8636](https://img.qammunity.org/2021/formulas/mathematics/college/5duyl10qif08bb2d73wtvu35xdvjzgboq0.png)