Question

A force acts on a 9.90 kg mobile object that moves from an initial position of to a final position of in 5.40 s. Find (a) the work done on the object by the force in the 5.40 s interval, (b) the average power due to the force during that interval, and (c) the angle between vectors and .

Answer 1

Given that,

Mass of object = 9.90 kg

Time =5.40 s

Suppose the force is (2.00i + 9.00j + 5.30k) N, initial position is (2.70i - 2.90j + 5.50k) m and final position is (-4.10i + 3.30j + 5.40k) m.

We need to calculate the displacement

Using formula of displacement

`s=r_(2)-r_(1)`

Where,
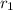`r_(1)` = initial position

`r_(2)` = final position

Put the value into the formula

`s= (-4.10i + 3.30j + 5.40k)-(2.70i - 2.90j + 5.50k)`

`s= -6.80i+6.20j-0.1k`

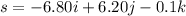
(a). We need to calculate the work done on the object

Using formula of work done

`W=F\cdot s`

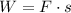
Put the value into the formula

`W=(2.00i + 9.00j + 5.30k)\cdot (-6.80i+6.20j-0.1k)`

`W=-13.6+55.8-0.53`

`W=41.67\ J`

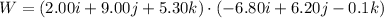
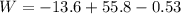
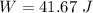
(b). We need to calculate the average power due to the force during that interval

Using formula of power

`P=(W)/(t)`

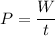
Where, P = power

W = work

t = time

Put the value into the formula

`P=(41.67)/(5.40)`

`P=7.71\ Watt`

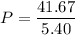
(c). We need to calculate the angle between vectors

Using formula of angle

`\theta=\cos^(-1)((r_(1)r_(2))/(|r_(1)||r_(2)|))`

Put the value into the formula

`\theta=\cos^(-1)((-4.10i + 3.30j + 5.40k)\cdot(2.70i - 2.90j + 5.50k))/(7.54*6.778))`

`\theta=79.7^(\circ)`

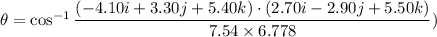
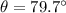
Hence, (a). The work done on the object by the force in the 5.40 s interval is 41.67 J.

(b). The average power due to the force during that interval is 7.71 Watt.

(c). The angle between vectors is 79.7°