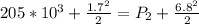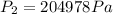Answer:
The velocity is
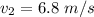
The pressure is
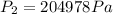
Step-by-step explanation:
From the question we are told that
The speed at which water is travelling through is
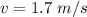
The pressure is
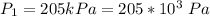
The diameter of the new pipe is
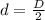
Where D is the diameter of first pipe
According to the principal of continuity we have that
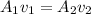
Now
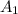 is the area of the first pipe which is mathematically represented as
is the area of the first pipe which is mathematically represented as
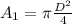
and
 is the area of the second pipe which is mathematically represented as
is the area of the second pipe which is mathematically represented as
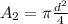
Recall
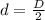
![A_2 = \pi ([ D^2])/(4 *4)](https://img.qammunity.org/2021/formulas/physics/college/mmivn22bvegjokfr0yqi8d8m80h6ljw0nw.png)
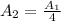
So
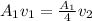
substituting value
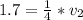
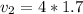
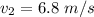
According to Bernoulli's equation we have that
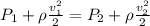
substituting values