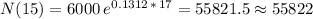Question

A culture started with 6,000 bacteria. After 2

hours, it grew to 7,800 bacteria. Predict how
many bacteria will be present after 15 hours.
Round your answer to the nearest whole
number.
P - Aekt

Answer 1

The population, after 15 hours grows from 6000 individuals to 42938 individuals.

Explanation:

Recall the formula for exponential growth:

`N(t)=N_0\,e^{k\,t|`

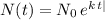
where the starting number of individuals in the population is
`N_0` (in our case 6000). "t" is the time in hours, and "k" is the rate of growth (unknown to us, but that we can find from the info they provide on how much the population grew in 2 hours.

The general exponential growth expression can then be written as:
`N(t)=6000\,e^{k\,t|`

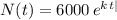
now imposing the 2 hour condition information:

`7800=6000\,e^(k\,*\,2)\\(7800)/(6000) =e^(k\,*\,2)\\1.3=e^(k\,*\,2)\\ln(1.3)=2\,k\\k=(ln(1.3))/(2) \\k=0.1312`

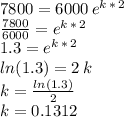
Now that we know the value of the rate of growth (k = 0.1312), we can estimate the population after 15 hours.

Now there is an important point here: If the question is what the population is after 15 hours from the starting 6,000 bacteria, then the answer is given by replacing t with 15 in the original formula:

`N(15)=6000\,e^(0.1312\,*\,15)=42938`

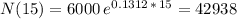
On the other hand, if you are asked for the population 15 hours after you saw the growth of bacteria to 7800 in 2 hours, then you need to find the population after 17 hours from the very starting point (6000 bacteria). This answer is associated with a little more tricky question but worth to have in mind:

`N(15)=6000\,e^(0.1312\,*\,17)=55821.5\approx 55822`