Answer:
Correct option: First one -> 16 mm
Explanation:
The equilateral triangle has its three sides with the same length.
So if the perimeter is 96 mm, we have:
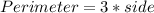
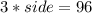
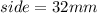
The segment MA is the height of the equilateral triangle, and its length can be calculated with the equation:
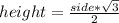
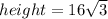
Using the Pythagoras' theorem in the triangle ACM, we have:
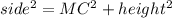
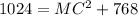
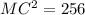
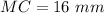
Correct option: First one