Answer:
a)
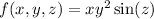
b)

Explanation:
Recall that given a function f(x,y,z) then
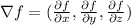 . To find f, we will assume it exists and then we will find its form by integration.
. To find f, we will assume it exists and then we will find its form by integration.
First assume that F =
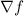 . This implies that
. This implies that
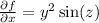 if we integrate with respect to x we get that
if we integrate with respect to x we get that
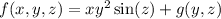 for some function g(y,z). If we take the derivative of this equation with respect to y, we get
for some function g(y,z). If we take the derivative of this equation with respect to y, we get
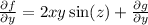
This must be equal to the second component of F. Then
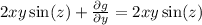
This implies that
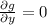 , which means that g depends on z only. So
, which means that g depends on z only. So
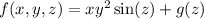
Taking the derivative with respect to z and making it equal to the third component of F, we get
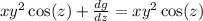
which implies that
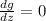 which means that g(z) = K, where K is a constant. So
which means that g(z) = K, where K is a constant. So
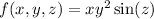
b) To evaluate
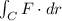 we can evaluate it by using f. We can calculate the value of f at the initial and final point of C and the subtract them as follows.
we can evaluate it by using f. We can calculate the value of f at the initial and final point of C and the subtract them as follows.
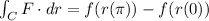
Recall that
 so
so
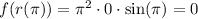
Also
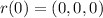 so
so
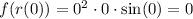
So
