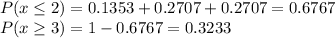Answer:

Explanation:
If the number of defects in poured metal follows a Poisson distribution, the probability that x defects occurs is:
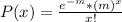
Where x is bigger or equal to zero and m is the average. So replacing m by 2, we get that the probability is equal to:
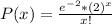
Finally, the probability that there will be at least three defects in a randomly selected cubic millimeter of this metal is equal to:

Where
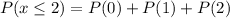
So, P(0), P(1) and P(2) are equal to:

Finally,
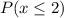 and
and
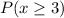 are equal to:
are equal to: