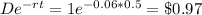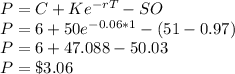Question

The price of a European call option on a stock with a strike price of $50 is $6. The stock price is $51, the continuously compounded risk-free rate (all maturities) is 6% and the time to maturity is one year. A dividend of $1 is expected in six months. What is the price of a one-year European put option on the stock with a strike price of $50?

Answer 1

$3.06

Step-by-step explanation:

The put call parity shows the relationship between the price of European put options and European call options of the same strike price and expiry date.

Given that:

Strike price (K) = $50

Price (C) = $6

rate (r) = 6% = 0.06

Stock price (SO) = $51

Time (T) = 1 year

Dividend (D) = $1

The period of dividend (t) = 6 months = 0.5 years

The put call parity (P) is given by the equation:

`P+SO=C+Ke^(-rT)\\P=C+Ke^(-rT)-SO`

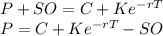
The dividend present value =
`De^(-rt)=1e^(-0.06*0.5)=\$0.97`

`P=C+Ke^(-rT)-SO\\P=6+50e^(-0.06*1)-(51-0.97)\\P=6+47.088-50.03\\P=\$3.06`