Question

Based on aâ poll, among adults who regret gettingâ tattoos, 18â% say that they were too young when they got their tattoos. Assume that eight adults who regret getting tattoos are randomlyâ selected, and find the indicated probability. Complete partsâ (a) throughâ (d) below.

a. Find the probability that none of the selected adults say that they were too young to get tattoos.
b. Find the probability that exactly one of the selected adults says that he or she was too young to get tattoos.
c. Find the probability that the number of selected adults saying they were too young is 0 or 1.
d. It we randomly select 9 adults. Is 1 a significantly low number who day that they were too young to get tattoos?

Answer 1

a) 20.44% probability that none of the selected adults say that they were too young to get tattoos.

b) 35.90% probability that exactly one of the selected adults says that he or she was too young to get tattoos.

c) 56.34% probability that the number of selected adults saying they were too young is 0 or 1.

d) No

Explanation:

For each adult, there are only two possible outcomes. Either they say they were too young when they got their tattoos, or they don't say that. Each adult is independent of each other. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

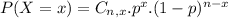
In which
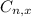`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

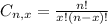
And p is the probability of X happening.

18% say that they were too young when they got their tattoos.

This means that
`p = 0.18`

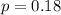
Eight adults who regret getting tattoos are randomly selected

This means that
`n = 8`

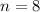
a. Find the probability that none of the selected adults say that they were too young to get tattoos.

This is P(X = 0).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(8,0).(0.18)^(0).(0.82)^(8) = 0.2044`

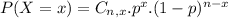
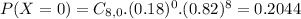
20.44% probability that none of the selected adults say that they were too young to get tattoos.

b. Find the probability that exactly one of the selected adults says that he or she was too young to get tattoos.

This is P(X = 1).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 1) = C_(8,1).(0.18)^(1).(0.82)^(7) = 0.3590`

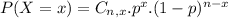
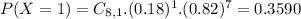
35.90% probability that exactly one of the selected adults says that he or she was too young to get tattoos.

c. Find the probability that the number of selected adults saying they were too young is 0 or 1.

Either a. or b.

20.44 + 35.90 = 56.34

56.34% probability that the number of selected adults saying they were too young is 0 or 1.

d. It we randomly select 9 adults. Is 1 a significantly low number who day that they were too young to get tattoos?

Now
`n = 9`

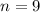
It is significantly low if it is more than 2.5 standard deviations below the mean.

The mean is
`E(X) = np = 9*0.18 = 1.62`

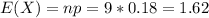
The standard deviation is
`√(V(X)) = √(n*p*(1-p)) = √(9*0.18*0.82) = 1.15`

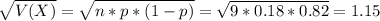
1 > (1.62 - 2.5*1.15)

So the answer is no.