Question

A 54.0 kg ice skater is gliding along the ice, heading due north at 4.10 m/s . The ice has a small coefficient of static friction, to prevent the skater from slipping sideways, but Uk = 0. Suddenly, a wind from the northeast exerts a force of 3.70 N on the skater.a) Use work and energy to find the skater's speed after gliding 100 m in this wind.b) What is the minimum value of Ug that allows her to continue moving straight north?

Answer 1

a. 2.668 m/s

b. 0.00494

Step-by-step explanation:

The computation is shown below:

a. As we know that

`W = F* d`

`KE = 0.5* m* v^2`

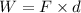
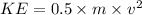
As the wind does not move the skater to the east little work is performed in this direction. All the work goes in the direction of the N-S. And located in that direction the component of the Force.

F = 3.70 cos 45 = 2.62 N

`W = F * d = 2.62 N * 100 m`

`W = 261.6 N* m`

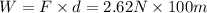
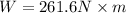
We know that

KE1 = Initial kinetic energy

KE2 = kinetic energy following 100 m

The energy following 100 meters equivalent to the initial kinetic energy less the energy lost to the work performed by the wind on the skater.

So, the equation is

KE2 = KE1 - W

`0.5 m* v2^2 = 0.5 m\ v1^2 - W`

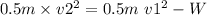
Now solve for v2

`v2 = \sqrt{v1^2 - {(2W)/(M)}}`

`= \sqrt{4.1 m/s)^2 - (2 * 261.6 N* m)/(54.0 kg)}`

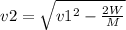
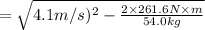
= 2.668 m/s

b. Now the minimum value of Ug is

As we know that

Ff = force of friction

Us = coefficient of static friction

N = Normal force = weight of skater

So,

`Ff = Us* N`

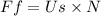
Now solve for Us

`= (Ff)/(N)`

`= (3.70 N * cos 45 )/(54.0 kg * 9.81 m/s^2)`

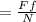
= 0.00494