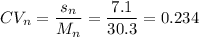Answer:
The group that has greater value of relative dispersion is the smokers group, as the coefficient of variationof their data is bigger than the coefficient of variation of the non-smokers group data.
CV smokers: 0.387
CV non-smokers: 0.234
Explanation:
We will calculate the relative dispersion of each data set with its coefficient of variation (ratio of the standard deviation to the arithmetic mean).
Then, first we calculate the mean and standard deviation for the smokers data:
Mean: 43.7
Standard deviation: 286.5
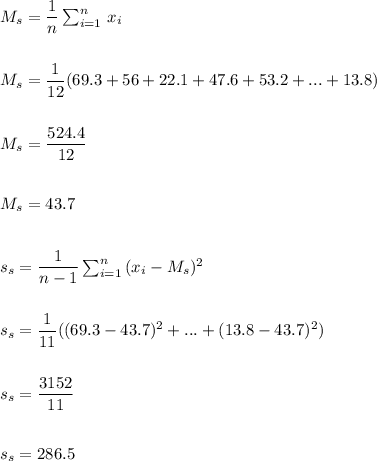
The mean and standard deviation for the non-smokers is:
Mean: 30.3
Standard deviation: 50.9
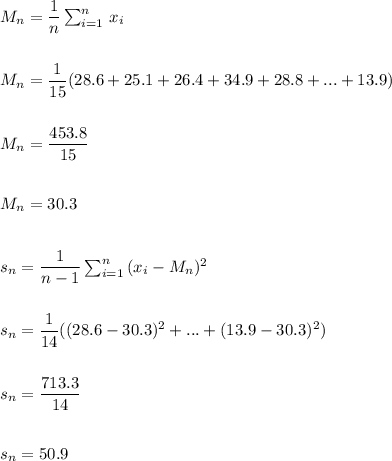
Now, we can calculate the coefficient of variation:
CV smokers:
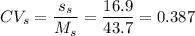
CV non-smokers: