Question

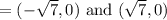
Find the center, vertices, and foci of the ellipse with equation 3x2 + 7y2 = 21.

Answer 1

Center
`= (0,0)`

Vertices
`=(-√(7),0)\text{ and }(√(7),0)`

Foci
`=(-2,0)\text{ and }(2,0)`.

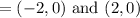Explanation:

The standard form of an ellipse is

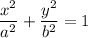`(x^2)/(a^2)+(y^2)/(b^2)=1` ...(1)

where, a>b, (0,0) is center, (±a,0) are vertices and (±c,0) are foci.

`c=√(a^2-b^2)`

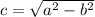
The given equation of ellipse is

`3x^2+7y^2=21`

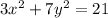
Divide both sides by 21.

`(3x^2+7y^2)/(21)=(21)/(21)`

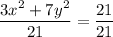
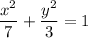`(x^2)/(7)+(y^2)/(3)=1` ...(2)

On comparing (1) and (2), we get

`a^2=7,b^2=3`

`a=√(7),b=√(3)`

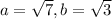
Now,

`c=√(a^2-b^2)=√(7-3)=√(4)=2`

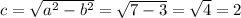
Therefore,

Center
`= (0,0)`

Vertices
`=(\pm a,0)=(\pm √(7),0}=(-√(7),0)\text{ and }(√(7),0)`

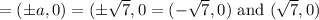
Foci
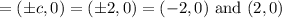`=(\pm c, 0)=(\pm 2,0)=(-2,0)\text{ and }(2,0)`.