Question

Suppose that 40 percent of the drivers stopped at State Police checkpoints in Storrs on Spring Weekend show evidence of driving while intoxicated. Consider a sample of 5 drivers. a. Find the probability that none of the drivers shows evidence of intoxication. b. Find the probability that at least one of the drivers shows evidence of intoxication. c. Find the probability that at most two of the drivers show evidence of intoxication. d. Find the probability that more than two of the drivers show evidence of intoxication. e. What is the expected number of intoxicated drivers

Answer 1

a) 0.778

b) 0.9222

c) 0.6826

d) 0.3174

e) 2 drivers

Explanation:

Given:

Sample size, n = 5

P = 40% = 0.4

a) Probability that none of the drivers shows evidence of intoxication.

`P(x=0) = ^nC_x P^x (1-P)^n^-^x`

`P(x=0) = ^5C_0 (0.4)^0 (1-0.4)^5^-^0`

`P(x=0) = ^5C_0 (0.4)^0 (0.60)^5`

`P(x=0) = 0.778`

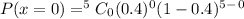
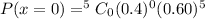
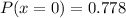
b) Probability that at least one of the drivers shows evidence of intoxication would be:

P(X ≥ 1) = 1 - P(X < 1)

`= 1 - P(X = 0)`

`= 1 - ^5C_0 (0.4)^0 * (0.6)^5`

`= 1 - 0.0778`

`= 0.9222`

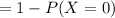
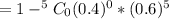
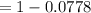
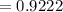
c) The probability that at most two of the drivers show evidence of intoxication.

P(x≤2) = P(X = 0) + P(X = 1) + P(X = 2)

`^5C_0 (0.4)^0 (0.6)^5 + ^5C_1 (0.4)^1 (0.6)^4 + ^5C_2 (0.4)^2 (0.6)^3`

`= 0.6826`

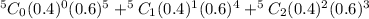
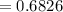
d) Probability that more than two of the drivers show evidence of intoxication.

P(x>2) = 1 - P(X ≤ 2)

`= 1 - [^5C_0 (0.4)^0 (0.6)^5 + ^5C_1 (0.4)^1 (0.6)^4 + ^5C_2 * (0.4)^2 (0.6)^3]`

`= 1 - 0.6826`

`= 0.3174`

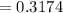
e) Expected number of intoxicated drivers.

To find this, use:

Sample size multiplied by sample proportion

n * p

= 5 * 0.40

= 2

Expected number of intoxicated drivers would be 2