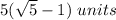Question

Given a rectangle with the following dimensions: Area = 100 units squared Length = x + 10 units Width = x units Find the value of x by completing the square method

Answer 1

The value of x is:
`5 (\sqrt5-1)\ units`

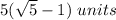
Explanation:

Given that:

Area of rectangle = 100 sq units

Length = (x+10) units

Width = x units

We know that area of a rectangle is given by the formula:

`A = l * w`

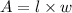
Where l is length of rectangle and

w is the width of rectangle

Putting the values in formula:

`x(x+10) = 100\\\Rightarrow x^2+10x=100\\\text{Trying to make square on both sides by Adding 25 on both sides}:\\\Rightarrow x^2+10x+25=100+25\\\Rightarrow x^2+2 * 5 * x+5^2=125\\\text{Formula: } a^(2) +2 * a * b+ b^(2) = (a+b)^2\\\Rightarrow (x+5)^2 = 25 * 5\\\text{Taking square root on both sides:}\\\Rightarrow (x+5) = 5\sqrt5\\\Rightarrow x = 5\sqrt5-5\\\Rightarrow x = 5 (\sqrt5-1)`

So, The value of x is:
`5 (\sqrt5-1)\ units`