Question

Two large rectangular aluminum plates of area 180 cm2 face each other with a separation of 3 mm between them. The plates are charged with equal amount of opposite charges, ±17 µC. The charges on the plates face each other. Find the flux (in N · m2/C) through a circle of radius 3.3 cm between the plates when the normal to the circle makes an angle of 4° with a line perpendicular to the plates. Note that this angle can also be given as 180° + 4°. N · m2/C

Answer 1

Φ = 361872 N.m^2 / C

Step-by-step explanation:

Given:-

- The area of the two plates,
`A_p = 180 cm^2`

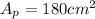
- The charge on each plate,
`q = 17 * 10^-^6 C`

- Permittivity of free space,
`e_o = 8.85 * 10^-^1^2 (C^2)/(N.m^2)`

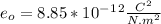
- The radius for the flux region,
`r = 3.3 cm`

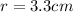
- The angle between normal to region and perpendicular to plates, θ = 4°

Find:-

Find the flux (in N · m2/C) through a circle of radius 3.3 cm between the plates.

Solution:-

- First we will determine the area of the region ( Ar ) by using the formula for the area of a circle as follows. The region has a radius of r = 3.3 cm:

`A_r = \pi *r^2\\\\A_r = \pi *(0.033)^2\\\\A_r = 0.00342 m^2`

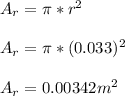
- The charge density ( σ ) would be considered to be uniform for both plates. It is expressed as the ratio of the charge ( q ) on each plate and its area ( A_p ):

σ =
`(q)/(A_p) = (17*10^-^6)/(0.018) \\`

σ = 0.00094 C / m^2

- We will assume the electric field due to the positive charged plate ( E+ ) / negative charged plate ( E- ) to be equivalent to the electric field ( E ) of an infinitely large charged plate with uniform charge density.

`E+ = E- = (sigma)/(2*e_o) \\\\`

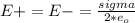
- The electric field experienced by a region between two infinitely long charged plates with uniform charge density is the resultant effect of both plates. So from the principle of super-position we have the following net uniform electric field ( E_net ) between the two plates:

`E_n_e_t = (E+) + ( E-)\\\\E_n_e_t = (0.00094)/(8.85*10^-^1^2) \\\\E_n_e_t = 106214689.26553 (N)/(C) \\`

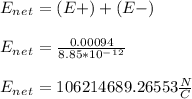
- From the Gauss-Law the flux ( Φ ) through a region under uniform electric field ( E_net ) at an angle of ( θ ) is:

Φ = E_net * Ar * cos ( θ )

Φ = (106214689.26553) * (0.00342) * cos ( 5 )

Φ = 361872 N.m^2 / C