Question

Determine if triangle DEF with coordinates D(2,1), E(3,5), and F (6,2) is an equilateral triangle. Use evidence to support your claim

Answer 1

No it is isosoles

Explanation:

Answer 2

No, it is isosceles.

Explanation:

(In assumption that the points have been plotted on a graph)

After the points have been plotted we need to find the distance between each set of points. DE, DF, and, EF.

Finding DE and DF

To find DE and DF, we need to do some counting. From point D to point E, we travel 2 units right, and 8 units up forming an imaginary triangle with a right angle. From D to F, we again travel 8 units right and 2 units up, forming the same triangle, just oriented slightly differently.

Using the Pythagorean Theorem (
`a^2 + b^2 =c^2`) we can plug in some values to find C and two of our side lengths.

`a^2+b^2=c^2`

`2^2+8^2=c^2`

`4 + 64 = c^2`

`68=c^2`

`√(68) =c`

`8.25=c`

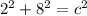
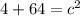
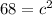
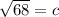
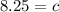
The lengths of DE and DF are both roughly 8.25

Finding EF

Finding EF is going to be the same process but just a little different.

If we start at E and travel to F, we move down 6 units and right 6 units, forming another right triangle. now we use the Pythagorean Theorem (
`a^2 + b^2 =c^2`) again, to find C and the length of EF.

`a^2 + b^2 =c^2`

`6^2+6^2=c^2`

`36+36=c^2`

`72=c^2`

`√(72) =c`

`8.49=c`

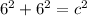
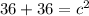
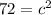
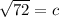
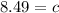
The length of EF is roughly 8.49 units.

Since not all of the sides of the triangle are the length, triangle DEF is not equilateral. Instead triangle DEF is isosceles.