Question

An aluminum bar 600mm long, with diameter 40mm long has a hole drilled in the center of the bar.The hole is 30mm in diameter and is 100mm long. If modulus of elasticity for the aluminum is 85GN/m2.Calculate the total contraction on the bar due to a compressive load in 180KN

Answer 1

Total contraction on the Bar = 1.22786 mm

Step-by-step explanation:

Given that:

Total Length for aluminum bar = 600 mm

Diameter for aluminum bar = 40 mm

Hole diameter = 30 mm

Hole length = 100 mm

elasticity for the aluminum is 85GN/m² = 85 × 10³ N/mm²

compressive load P = 180 KN = 180 × 10³ N

Calculate the total contraction on the bar = ???

The relation used in calculating the contraction on the bar is:

`\delta L = (P *L )/(A*E)`

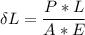
The relation used in calculating the total contraction on the bar can be expressed as :

Total contraction in the Bar = (contraction in part of bar without hole + contraction in part of bar with hole)

i.e

Total contraction on the Bar =
`(P *L_1 )/(A_1*E) + (P *L_2 )/(A_2 *E)`

Let's find the area of cross section without the hole and with the hole

Area of cross section without the hole is :

Using A = πd²/4

A = π (40)²/4

A = 1256.64 mm²

Area of cross section with the hole is :

A = π (40²-30²)/4

A = 549.78 mm²

Total contraction on the Bar =
`(P *L_1 )/(A_1*E) + (P *L_2 )/(A_2 *E)`

Total contraction on the Bar =
`(180 *10^3 \N )/(85*10^3 \ N/mm^2) [(500)/(1256.64)+ (100)/(549.78)]`

Total contraction on the Bar = 2.117( 0.398 + 0.182)

Total contraction on the Bar = 2.117*(0.58)

Total contraction on the Bar = 1.22786 mm