Question

A multiple-choice examination has 20 questions, each with five possible answers, only one of which is correct. Suppose that one of the students who takes the examination answers each of the questions with an independent random guess. What is the probability that he answers at least seventeen questions correctly? (Round your answer to three decimal places.)

Answer 1

The probability that the student answers at least seventeen questions correctly is
`8.03* 10^(-10)`.

Explanation:

Let the random variable X represent the number of correctly answered questions.

It is provided all the questions have five options with only one correct option.

Then the probability of selecting the correct option is,

`P(X)=p=(1)/(5)=0.20`

There are n = 20 question in the exam.

It is also provided that a student taking the examination answers each of the questions with an independent random guess.

Then the random variable can be modeled by the Binomial distribution with parameters n = 20 and p = 0.20.

The probability mass function of X is:

`P(X=x)={20\choose x}\ 0.20^(x)\ (1-0.20)^(20-x);\ x =0,1,2,3...`

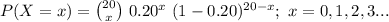
Compute the probability that the student answers at least seventeen questions correctly as follows:

`P(X\geq 17)=P (X=17)+P (X=18)+P (X=19)+P (X=20)`

`=\sum\limits^(20)_(x=17){{20\choose x}\ 0.20^(x)\ (1-0.20)^(20-x)}\\\\=0.00000000077+0.000000000032+0.00000000000084+0.000000000000042\\\\=0.000000000802882\\\\=8.03*10^(-10)`

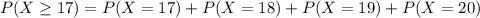
Thus, the probability that the student answers at least seventeen questions correctly is
`8.03* 10^(-10)`.