Question

Based on a​ survey, assume that 43​% of consumers are comfortable having drones deliver their purchases. Suppose we want to find the probability that when five consumers are randomly​ selected, exactly two of them are comfortable with the drones. What is wrong with using the multiplication rule to find the probability of getting two consumers comfortable with drones followed by three consumers not​ comfortable, as in this​ calculation: (0.43 )(0.43 )(0.57 )(0.57 )(0.57 )equals0.0342​?

Answer 1

The probability of getting two consumers comfortable with drones is 0.3424.

Explanation:

The probability that a consumer is comfortable having drones deliver their purchases is, p = 0.43.

A random sample of n = 5 consumers are selected, and exactly x = 2 of them are comfortable with the drones.

To compute the probability of getting two consumers comfortable with drones followed by three consumers not​ comfortable, we will use the Binomial distribution instead of the multiplication rule to find the probability.

This is because in this case we need to compute the number of possible combinations of two consumers who are comfortable with drones.

So, X = number of consumers comfortable with drones, follows a Binomial distribution with parameters n = 5 and p = 0.43.

Compute the probability of getting two consumers comfortable with drones as follows:

`P(X=x)={5\choose x}\ 0.43^(x)\ (1-0.43)^(5-x);\ x=0,1,2,3...`

`P(X=2)={5\choose 2}\ 0.43^(2)\ (1-0.43)^(5-2)`

`=10* 0.1849* 0.185193\\=0.342421857\\\approx 0.3424`

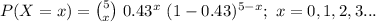
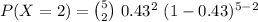
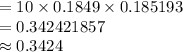
Thus, the probability of getting two consumers comfortable with drones is 0.3424.