Answer:
Evaluate f(7)
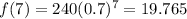
Determine x when f(×)=120
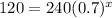
We can derive both sides by 240 and we got:
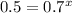
Now we can apply natural log on both sides and we got:
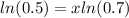
And if we solve for the value of x we got:
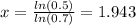
And then the value of x = 1.943
Explanation:
We have the following function given:
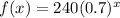
Evaluate f(7)
And we want to find
 so we just need to replace x=7 and we got:
so we just need to replace x=7 and we got:
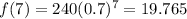
Determine x when f(×)=120
And for the second part we want to find a value of x who satisfy that the function would be equal to 120 and we can set up this:
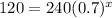
We can derive both sides by 240 and we got:
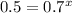
Now we can apply natural log on both sides and we got:
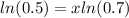
And if we solve for the value of x we got:
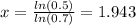
And then the value of x = 1.943