Answer: See below
Step-by-step explanation:
1. To calculate the mass, you know you can convert by using molar mass. Since mass is in grams, we can use molar mass to convert moles to grams. This calls for the Ideal Gas Law.
Ideal Gas Law: PV=nRT
We manipulate the equation so that we are solving for moles, then convert moles to grams.
n=PV/RT
P= 100 kPa
V= 0.831 L
R= 8.31 kPa*L/mol*K
T= 27°C+273= 300 K
Now that we have our values listed, we can plug in to find moles.
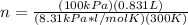
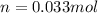
We use the molar mass of NO₂ to find grams.
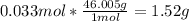
The mass is 1.52 g.
2. To calculate the temperature, we need to use the Ideal Gas Law.
Ideal Gas Law: PV=nRT
We can manipulate the equation so that we are solving for temperature.
T=PV/nR
P= 700.0 kPa
V= 33.2 L
R= 8.31 kPa*L/mol*K
n= 70 mol
Now that we have our values, we can plug in and solve for temperature.
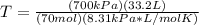
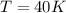
The temperature is 40 K.