Question

A mean score of driving exam for a group of drivers education students 72 points with a standard deviation of 5 points. Apply Chebychev's theorem to the data using K=2

Answer 1

At least the 75% of the scores of driving exams are between 62 and 82 points.

Explanation:

The chebyshev theorem said that the proportion of any distribution that is less than k deviations of the mean is at least
`1-(1)/(k^2)`.

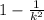So, if we replace k by 2, we can calculated the limits as:

`x+2s=72+2(5)=82\\x-2s=72-2(5)=62`

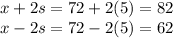
Where x is the mean and s is the standard deviation.

Then,
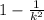`1-(1)/(k^2)` is equal to:

`1-(1)/(k^2)=1-(1)/(2^2)=0.75`

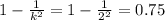
It means that at least the 75% of the scores of driving exams are between 62 and 82 points.