Answer:
2.2 metres squared
Explanation:
We need to find the area of this trapezoid.
The area of a trapezoid is denoted by:
 , where
, where
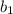 and
and
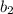 are the parallel bases and h is the height
are the parallel bases and h is the height
Here, we already know the lengths of the two bases; they are 0.9 metres and 2.3 metres. However, we need to find the length of the height.
Notice that one of the angles is marked 45 degrees. Let's draw a perpendicular line from top endpoint of the segment labelled 0.9 to the side labelled 2.3. We now have a 45-45-90 triangle with hypotenuse 2.0 metres. As one of such a triangle's properties, we can divide 2.0 by √2 to get the length of both legs:
2.0 ÷ √2 = √2 ≈ 1.414 ≈ 1.4
Thus, the height is h = 1.4 metres. Now plug all these values we know into the equation to find the area:

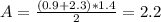
The answer is thus 2.2 metres squared.
~ an aesthetics lover