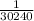Question

A student identification card consists

of 5 digits selected from 10 possible
digits from 0 to 9. Digits cannot be
repeated. Find the probability that
randomly generated card has the
exact number 94213.

Answer 1

`(1)/(30240)`

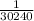
Explanation:

Given

ID Card of 5 digits

Possibly Digits = {0,1...,9}

Required

Probability that a card has exact number 94213

First, we have o determine the total possible number of ID card numbers

Let the card number be represented by ABCDE

Given that repetition of digits is not allowed;

A can be any of 10 digits

B can any of the remaining 9 digits

C can be any of the remaining 8 digits

D can be any of the remaining 7 digits

E can be any of the remaining 6 digits

Total number of cards = 10 * 9 *8 * 7 * 6

Total = 30240

Provided that the card number is generated at random; each card number has the same probability of
`(1)/(30240)`

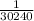
Hence, the probability of having 94213 is
`(1)/(30240)`