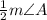Question

In the figure alongside, BP and CP are angular bisectors of the exterior angles BCD and CBE of angle ABC. prove that angle BPC = 90°- angle A divided by 2​

Answer 1

Explanation:

From the figure attached,

CP is an angle bisector of angle BCD and BP is the angle bisector of angle CBE

Therefore, m∠DCP ≅ m∠BCP

and m∠PBE ≅ m∠PBC

m∠A + m∠CBA = m∠BCD

m∠A + (180° - m∠CBE) = m∠BCD

m∠A + 180° = m∠CBE + m∠BCD

m∠A + 180° = 2(m∠PCB) + 2(m∠PBC) [Since m∠CBE = 2m∠PCB and m∠BCD = 2(m∠PBC)

m∠A + 180° = 2(m∠PCB + m∠PBC)

m∠A + 180° = 2(180° - m∠BPC) [Since m∠PCB + m∠PBC + m∠BPC = 180°]

`[(1)/(2)(m\angle A)]+90=180 - m\angle BPC`

m∠BPC = 180 -
`[(1)/(2)(m\angle A)]-90`

m∠BPC = 90 -
`(1)/(2)m\angle A`