Answer:
98 g
Step-by-step explanation:
Start with the balanced equation. Then, make a little chart under the equation showing the information you have and need.
3O₂(g) + 4Al(s) → 2Al₂O₃(s)
m ? 110 g
M ___ ____
n ___ <= ____
"m" is for mass. "M" is for molar mass (some teachers use "MM"). "n" is for the number of moles.
To find the mass of oxygen:
- Calculate the molar mass of oxygen (
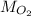 )
) - Calculate molar mass of aluminum (
 )
) - Use
 to find the moles of aluminum (
to find the moles of aluminum (
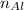 )
) - With
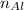 , use the mole ratio to find the moles of oxygen (
, use the mole ratio to find the moles of oxygen (
 )
) - Use
 and
and
 to find the mass of oxygen (
to find the mass of oxygen (
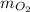 )
)
To find molar mass, use the atomic mass on your periodic table. For each atom of an element, add on its atomic mass.
Molar mass of aluminum (one Al atom):
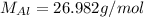
Molar mass of oxygen (two O atoms):
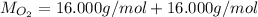
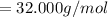
Update the chart:
3O₂(g) + 4Al(s) → 2Al₂O₃(s)
m ? 110 g
M 32.000 g/mol 26.982 g/mol
n ___ <= ____
Find the moles of aluminum
 Multiply mass by molar mass to find moles.
Multiply mass by molar mass to find moles.
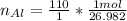 The units "g" cancel out.
The units "g" cancel out.
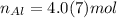 Keep one extra significant figure. (110 has 2 sig. figs.)
Keep one extra significant figure. (110 has 2 sig. figs.)
3O₂(g) + 4Al(s) → 2Al₂O₃(s)
m ? 110 g
M 32.000 g/mol 26.982 g/mol
n ___ <= 4.0(7) mol
Find the moles of oxygen using the mole ratio, which comes from the coefficients in the balanced equation.
The mole ratio of oxygen to aluminum is 3 to 4.
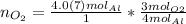 Multiply moles of aluminum by the mole ratio.
Multiply moles of aluminum by the mole ratio.
 "molAl" units cancel out.
"molAl" units cancel out.
 Keep two sig. figs. when the first is a "5"
Keep two sig. figs. when the first is a "5"
3O₂(g) + 4Al(s) → 2Al₂O₃(s)
m ? 110 g
M 32.000 g/mol 26.982 g/mol
n 3.0(52) mol <= 4.0(7) mol
Find the mass of oxygen
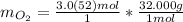 Multiply moles by molar mass.
Multiply moles by molar mass.
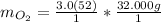 The "mol" unit cancels out.
The "mol" unit cancels out.
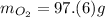 Keep one sig. fig. to round. "6" rounds up.
Keep one sig. fig. to round. "6" rounds up.
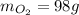 <= Final answer
<= Final answer
∴ 98 grams of oxygen are required to completely react with 110 grams of aluminum.