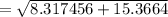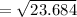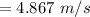Answer:
The correct answer will be:
(a) 2.884 m/s
(b) 0.4 s
(c) 1.154 m
(d) 4.867 m/s
Step-by-step explanation:
The given values are:
Mass, m = 500 g
on converting:
m = 0.5 kg
Force constant, k = 1200 N
Height, h = 0.8 m
x = 0.1 m
(a)...
As we know,
Kinetic Energy,

On putting the estimated values, we get


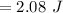
Now,
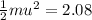
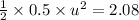
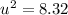
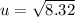
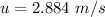
(b)...
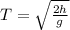
On putting the values, we get

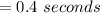
(c)...
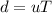
On putting the estimated values, we get
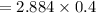
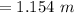
(d)...
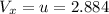
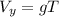
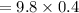

Now,

On putting the estimated values, we get