Question

Use the method of completing the square to write the equations of the given parabola in this form: (y-k)=a(x-h)^2 where a =0, (h,k) is the vertex, and x=h is the axis of symmetry. Find the vertex of this parabola: y=-x^2-2x-5

Answer 1

Explanation:

There are but a few rules we have to follow when completing the square. However, they are very important rules so we have to be careful. First and foremost, the coefficient on the x-squared term HAS to be a positive 1. If it is not, we have to manipulate the function so it is a positive 1. Then we take half the linear term, square it and add it to both sides (and sometimes this can be very tricky. It is tricky here, so pay attention.)

We begin by separating the x terms from the constant by setting the parabola equal to 0 and moving the constant:

`-x^2-2x=5`

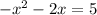
The coefficient on the x-squared is a negative 1, so we factor out the negative:

`-(x^2+2x)=5`

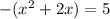
The linear term is 2. We take half of 2 which is 1, square 1 to get 1 and add it into the left side. BUT don't forget that we have a -1 out front of the ( ) refusing to be ignored. It is a multiplier. That means that we didn't add in a +1, we added in -1(1) which is -1. That is what we add to the right side:

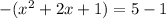`-(x^2+2x+1)=5-1` which simplifies to

`-(x^2+2x+1)=4`

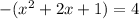
The reason for this process is that by completing the square you create a perfect square binomial on the left. We rewrite the parabola in terms of that perfect square binomial:

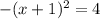`-(x+1)^2=4` which simplifies to

`-(x+1)^2-4=y`

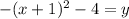
From this you can now determine that the vertex of the parabola is (-1, -4)