Question

The star Sirius has an apparent magnitude of -1.46 and appears 95-times brighter compared to the more distant star Tau Ceti, which has an absolute magnitude of 5.69

(a) Explain the terms apparent magnitude, absolute magnitude and bolometric magnitude.
(b) Calculate the apparent magnitude of the star Tau Ceti.
(c) Find the distance between the Earth and Tau Ceti

Answer 1

(a) Apparent magnitude is the perceived brightness of an astronomical object

Absolute magnitude is the luminosity based on viewing an object from a 32.6 light-years distance

Bolometric magnitude is the total emitted radiation of a star

(b) The apparent magnitude of the star Tau Ceti = 3.51

(c) The distance between the Earth and Tau Ceti is 1.13 × 10¹⁴ km

Step-by-step explanation:

(a) Apparent magnitude is an estimate of an astronomical objects' brightness as the object is perceived from the Earth

The absolute magnitude is the magnitude an object appears to have when viewed from a 32.6 light-years distance while having constant transfer of its luminosity that is not affected by cosmic dust and objects present in the line of sight

The bolometric magnitude of a star is the sum total of the star's radiation released over all electromagnetic spectrum wavelengths

(b) The apparent magnitude of the star Tau Ceti is found using the following equation;

`m_(2)-m_(1) = -2.512* log\left ((B_(2))/(B_(1)) \right )`

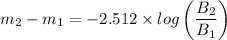
Where:

m₁ = Apparent magnitude of Tau Ceti

m₂ = Apparent magnitude of Sirius = -1.46

B₁ = Brightness of Tau Ceti

B₂ = Brightness of Sirius

`\left (B_(2))/(B_(1)) \right = 95`

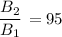
Hence we have;

`-1.46-m_(1) = -2.512* log\left (95 \right )`

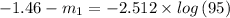
m₁ = -1.46 + 2.512 × log(95) = 3.51

The apparent magnitude of the star Tau Ceti = 3.51

(c) The distance between the Earth and Tau Ceti is found using the following equation;

`m-M = 5* log\left ((d)/(10) \right )`

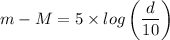
Where:

m = Apparent magnitude of Tau Ceti

M = Absolute magnitude of Tau Ceti = 5.69

d = The distance between the Earth and Tau Ceti

Which gives;

`3.51-5.69 = 5* log\left ((d)/(10) \right )`

`\therefore (d)/(10) = 10^(-0.436) = 0.3664`

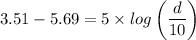
d = 10 × 0.3664 = 3.664 parsecs = 3.664 × 3.0857 × 10¹⁶ m

d = 1.13 × 10¹⁴ km.