Question

A corporation must appoint a​ president, chief executive officer​ (CEO), chief operating officer​ (COO), and chief financial officer​ (CFO). It must also appoint a planning committee with four different members. There are 14 qualified​ candidates, and officers can also serve on the committee.

A. How many different ways can the officers be​appointed?
B. How many different ways can the committee be​ appointed?
C. What is the probability of randomly selecting the committee members and getting the three youngest of the qualified​ candidates?

Answer 1

a) The officers can be appointed in 24024 different ways.

b) The committee can be appointed in 1001 different ways.

c) 1.1% probability of randomly selecting the committee members and getting the three youngest of the qualified​ candidates

Explanation:

The order in which the officers are appointed is important(the first is the president, second the CEO and so on...). So the permutations formula will be used.

Otherwise, in the committee there are no roles, so the order is not important. So the combinations formula will be used.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

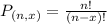
Combinations formula:

`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

A. How many different ways can the officers be ​appointed?

4 from a set of 14, with roles. So a permutation.

`P_((14,4)) = (14!)/((14-4)!) = 24024`

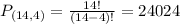
The officers can be appointed in 24024 different ways.

B. How many different ways can the committee be​ appointed?

4 from a set of 14, without roles. So combination

`C_(14,4) = (14!)/(4!(14-4)!) = 1001`

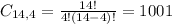
The committee can be appointed in 1001 different ways.

C. What is the probability of randomly selecting the committee members and getting the three youngest of the qualified​ candidates?

A probability is the number of desired outcomes divided by the number of total outcomes.

Desired outcomes.

The three youngest(1 combination), and one of the other 14-3 = 11. So
`D = 1*11 = 11`

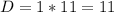
Total outcomes:

From B., 1001, so
`T = 1001`

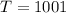
Probability:

`p = (D)/(T) = (11)/(1001) = 0.011`

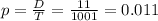
1.1% probability of randomly selecting the committee members and getting the three youngest of the qualified​ candidates