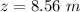Answer:
The distance covered by puck A before collision is
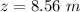
Step-by-step explanation:
From the question we are told that
The label on the two hockey pucks is A and B
The distance between the two hockey pucks is D 18.0 m
The speed of puck A is
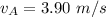
The speed of puck B is
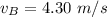
The distance covered by puck A is mathematically represented as
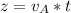
=>
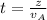
The distance covered by puck B is mathematically represented as

=>

Since the time take before collision is the same
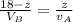
substituting values
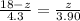
=>
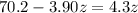
=>