Answer:
Explanation
Standard form
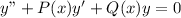
Hence your P(t) = -3, Q(t) = 2

After replacing all y", y' and y to homogeneous part, you will have
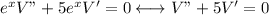 because
because
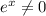
Let U = V'
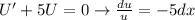 .
.
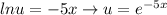
Replace back,

then
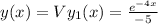
So, general solution of the ODE is

Particular solution is just take derivative of the general one twice and plug back into the original ODE to find A and B
You can finish it by yourself. Let me know if you need more help