Question

Charlie invests £1200 at 3.5% per annum compound interest.

Work out the value of Charlie's investment after 3 years.

Answer 1

£1,330.46

Explanation:

Using the compound interest formula
`A = P(1+(r)/(n) )^(nt)`

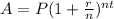
A = amount compounded after n years

P = principal (amount invested)

r = rate (in %)

t = time (in years)

n = time used to compound the money

Given P = £1200., r = 3.5%, t = 3years, n = 1 year(compounded annually)

`A = 1200(1+0.035)^(3)\\ A = 1200(1.035)^(3)\\ A = 1200* 1.108717875\\A = 1,330.46`

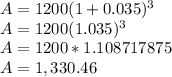
Value of Charlie's investment after 3 years is £1,330.46