Question

2. CTfastrak bus waiting times are uniformly distributed from zero to 20 minutes. Find the probability that a randomly selected passenger will wait the following times for a CTfastrak bus. b. Between 5 and 10 minutes. c. Exactly 7.5922 minutes. d. Exactly 5 minutes. e. Between 15 and 25 minutes.

Answer 1

b. 0.25

c. 0.05

d. 0.05

e. 0.25

Explanation:

if the waiting time x follows a uniformly distribution from zero to 20, the probability that a passenger waits exactly x minutes P(x) can be calculated as:

`P(x)=(1)/(b-a)=(1)/(20-0) =0.05`

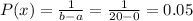
Where a and b are the limits of the distribution and x is a value between a and b. Additionally the probability that a passenger waits x minutes or less P(X<x) is equal to:

`P(X<x)=(x-a)/(b-a)=(x-0)/(20-0)=(x)/(20)`

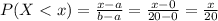
Then, the probability that a randomly selected passenger will wait:

b. Between 5 and 10 minutes.

`P(5<x<10) = P(x<10) - P(x<5)\\P(5<x<10) = (10)/(20) -(5)/(20)=0.25`

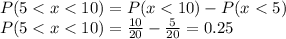
c. Exactly 7.5922 minutes

`P(7.5922)=0.05`

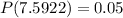
d. Exactly 5 minutes

`P(5)=0.05`

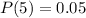
e. Between 15 and 25 minutes, taking into account that 25 is bigger than 20, the probability that a passenger will wait between 15 and 25 minutes is equal to the probability that a passenger will wait between 15 and 20 minutes. So:

`P(15<x<25)=P(15<x<20) \\P(15<x<20)=P(x<20) - P(x<15)\\P(15<x<20) = (20)/(20) -(15)/(20)=0.25`