Question

A commuter uses a bus and a train to get to work. The train is more than 5 minutes late 1/6 of the times they use it The bus is more than 5 minutes late 3/5 of the times they use it. What is the probability that both the bus and train will be more than 5 minutes late?

Answer 1

10% probability that both the bus and train will be more than 5 minutes late

Explanation:

Independent events:

If two events, A and B, are independent, we have that:

`P(A \cap B) = P(A)*P(B)`

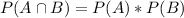
What is the probability that both the bus and train will be more than 5 minutes late?

The bus being more than 5 minutes late is independent of the train, and vice versa. So

Event A: Bus more than 5 minutes late

Event B: Train more than 5 minutes late

The train is more than 5 minutes late 1/6 of the times they use it

This means that
`P(B) = (1)/(6)`

The bus is more than 5 minutes late 3/5 of the times they use it.

This means that
`P(A) = (3)/(5)`

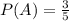
Then

`P(A \cap B) = (3)/(5)*(1)/(6) = (3)/(30) = 0.1`

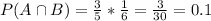
10% probability that both the bus and train will be more than 5 minutes late