Question

Office occupancy in a city is an indication of the economic health of the region in which it is located. A random sample of offices in two cities was​ selected, and the number of vacancies was recorded. The data are linked below. Construct a 99% confidence interval to estimate the difference in vacancy rates between these two cities. What conclusions can be made?

city 1 city 2
x1=22 x2=14
n1=165 n2=140

Answer 1

`(0.13-0.1) - 2.58 \sqrt{(0.13(1-0.13))/(165) +(0.10(1-0.10))/(140)}=-0.0664`

`(0.13-0.1) + 2.58 \sqrt{(0.13(1-0.13))/(165) +(0.10(1-0.10))/(140)}=0.124`

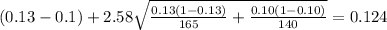
We are confident at 99% that the difference between the two proportions is between
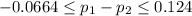`-0.0664 \leq p_1 -p_2 \leq 0.124` . And since the confidence interval cotains the value 0 we don't have enough evidence to conclude that we have significant differences between the to proportions in these two cities

Explanation:

`p_1` represent the real population proportion for 1

`\hat p_1 =(22)/(165)=0.13` represent the estimated proportion for 1

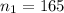`n_1=165` is the sample size required for 1

`p_2` represent the real population proportion for 2

`\hat p_2 =(14)/(140)=0.10` represent the estimated proportion for 2

`n_2=140` is the sample size required for 2

`z` represent the critical value for the margin of error

The confidence interval for the difference of two proportions would be given by this formula

`(\hat p_1 -\hat p_2) \pm z_(\alpha/2) \sqrt{(\hat p_1(1-\hat p_1))/(n_1) +(\hat p_2 (1-\hat p_2))/(n_2)}`

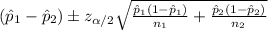
For the 99% confidence interval the significance is
`\alpha=1-0.99=0.01` and
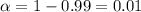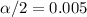`\alpha/2=0.005`, and the critical value using the normal standard distribution.

`z_(\alpha/2)=2.58`

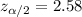
Replacing we got:

`(0.13-0.1) - 2.58 \sqrt{(0.13(1-0.13))/(165) +(0.10(1-0.10))/(140)}=-0.0664`

`(0.13-0.1) + 2.58 \sqrt{(0.13(1-0.13))/(165) +(0.10(1-0.10))/(140)}=0.124`

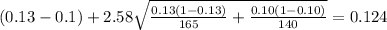
We are confident at 99% that the difference between the two proportions is between
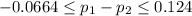`-0.0664 \leq p_1 -p_2 \leq 0.124` . And since the confidence interval cotains the value 0 we don't have enough evidence to conclude that we have significant differences between the to proportions in these two cities