Question

)A cable has a bandwidth of 3000 Hz assigned for data communication. The SNR is 3162. How many signal levels do we need?

Answer 1

`L=56.2`

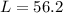
Step-by-step explanation:

We need to use two theoretical formulas: Shannon Capacity and Nyquist Bit Rate.

From Shannon:

`C=B*log_2(SNR+1)`

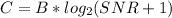
From Nyquist:

`C=2B*log_2(L)`

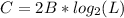
Where:

`C= Channel\hspace{3}capacity\\B=Bandwidth\hspace{3} of\hspace{3} the\hspace{3} channel\\SNR=Signal\hspace{3}to\hspace{3}noise\hspace{3}ratio\\L=Number\hspace{3}of\hspace{3}signal\hspace{3}levels\hspace{3}used\hspace{3}to\hspace{3}represent\hspace{3}data`

Using the data provided by the problem and the equations above, let's find the signal levels we need. Using the Shannon equation:

`C=B*log_2(SNR+1)`

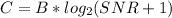
Where:

`B=3000Hz\\SNR=3162`

`C=3000*log_2(3162+1)\\\\C=3000*log_2(3163)\\\\C=34881.23352\hspace{3}bps`

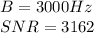
Now, using Nyquist equation:

`C=2B*log_2(L)`

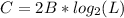
Where:

`C=34881.23352\hspace{3}bps\\B=3000Hz`

`34881.23352=2*3000*log_2(L)\\\\34881.23352=6000*log_2(L)`

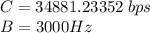
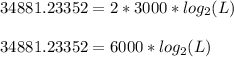
Solving for
`L` :

`(34881.23352)/(6000) =log_2(L)\\\\5.81353892=log_2(L)\\\\2^(5.81353892) =2^(log_2(L))\\ \\56.24055476=L\\\\L\approx56.2`

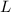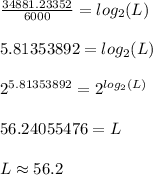
Therefore, we need approximately 56.2 signal levels.