Question

I can’t figure out the answer to this, does anybody know?

Answer 1

Option (2).

Explanation:

Let f(x) and g(x) are the two functions with domain A and B.

Then (fg)(x) will be the function with domain A∩B

(fg)(x) = f(x)g(x) Domain : A∩B

In this question two functions are,

c(x) =
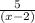`(5)/((x-2))` and d(x) = (x + 3)

Domain : (x - 2) > 0 ⇒ x > 2

and (x - 2) < 0 ⇒ x < 2

Or domain of (cd)(x) will be C = (-∞, 2)∪(2, ∞).

Similarly, d(x) = x + 3

Domain : All real numbers

: D = (-∞, ∞)

(cd)(x) = c(x)d(x)

=
`(5)/((x-2))* (x+3)`

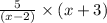
Domain of (cd)(x) will be,

Domain : C∩D = (-∞, 2)∪(2, ∞) ∩ (-∞, ∞)

: (-∞, 2) ∩ (2, ∞)

Therefore, domain of (cd)(x) will be all real values except 2.

Option (2) will be the answer.