Question

The largest z-score available in most tables is 2.99, which corresponds to a probability of 99.86%. A fair coin is

tossed 200 times.
a) What number of heads observedžwould correspond to a z-score of 2.99? [2]

Answer 1

The number of heads observed is 121.14 heads

Explanation:

The formula for the z-score of a proportion is given as follows;

`z=\frac{\hat{p}-p}{\sqrt{(pq)/(n)}}`

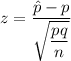
Where:

`{\hat{p}` = Sample proportion

p = Population success proportion = 0.5

q = 1 - p = 1 - 0.5 = 0.5

n = Number in of observation = 200

z = 2.99

Hence, we have;

`z=\frac{\hat{p}-0.5}{\sqrt{(0.5 * 0.5)/(200)}} = 2.99`

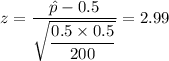
Therefore;

`{\hat{p}-0.5}{} = 2.99 * \sqrt{(0.5 * 0.5)/(200)} = 2.99 *(√(2) )/(40)`

`{\hat{p}` = 0.6057

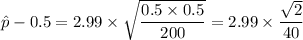
`Whereby \ \hat p = (Number \ of \ heads)/(Number \ of \ observation) = (Number \ of \ heads)/(200) = 0.6057`

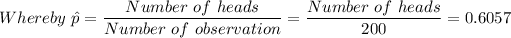
∴ The number of heads observed = 200 × 0.6057 = 121.14 heads.