Question

One of the advantages of skates is that they allow you to push against ice, which typically has low friction. Let’s consider an hockey player on frictionless ice who is going to shoot a slap shot. The player weighs Mp = 100kg. He is going to fire the puck, which weighs Mpuck = 0.5kg with a velocity of v = 50(m/s). How fast does the hockey player recoil in the direction opposite to the puck’s trajectory. If the force he exerts on the puck occurs over a time, ∆t = 0.1s what is the average force needed to create the impulse that accelerates the puck to that velocity?

Answer 1

a) v1f = 0.25 m/s

b) F = 50000N

Step-by-step explanation:

a) In order to calculate the speed of the player after he fires the puck, you use the conservation of momentum law. Before the puck is in motion and after the total momentum of both player and puck must conserve:

`m_1v_(1i)+m_2v_(2i)=m_1v_(1f)+m_2v_(2f)` (1)

m1: mass of the player = 100kg

v1i: initial velocity of the player = 0m/s

v2f: final velocity of the puck = ?

m2: mass of the puck = 0.5kg

v2i: initial velocity of the puck = 0 m/s

v2f: final velocity of the puck = 50 m/s

You replace these values into equation (1) and you solve for v1f (final velocity of player):

`0kgm/s+0kgm/s=(100kg)v_(1f)+(0.5kg)(50m/s)\\\\v_(1f)=-((0.5kg)(50m/s))/(100kg)\\\\v_(1f)=-0.25(m)/(s)`

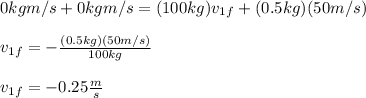
The minus sign means that player moves in a opposite direction to the motion of the puck

The velocity of the player after he fires the puck is 0.25 m/s

b) The force needed is given by the change in time , of the momentum of the player, which is given by:

`F=(\Delta p)/(\Delta t)=m(\Delta v)/(\Delta t)`

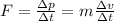
The change on the velocity of the puck is 50m/s, and the time interval is 0.1s.

`F=(100kg)(50m/s)/(0.1s)=50000N`

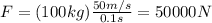
The force needed to create the needed impulse, to accelerate the puck is 50000N