Question

The Difference of Square: a^2 - b^2 = (a + b)(a - b)

Sara did a question as: 2x^2 - 2y^2 = (2x + 2y)(2x - 2y).


What's wrong with Sara's work? How to fix it?

Answer 1

`2x^2 - 2y^2 = 2(x - y)(x + y)`

Explanation:

Given

Difference of two squares:
`a^2 - b^2 = (a + b)(a - b)`

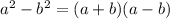
Sara Solution to a question:
`2x^2 - 2y^2 = (2x + 2y)(2x - 2y).`

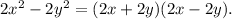
Required

State what's wrong with Sara's work

How to fix it

In Sara's solution, the coefficient of x and y is 2. Sara's solution is wrong because she included the coefficients of x and y when converting the expression to difference of two squares.

To fix this, the very first thing that needs to done is to factorize the given expression (as follows)

`2x^2 - 2y^2 = 2(x^2 - y^2)`

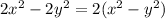
Then the difference of two squares can be applied on the expression in bracket. This gives

`2x^2 - 2y^2 = 2(x - y)(x + y)`