Question

(3xy)^2x^4y simplifying an expression

Answer 1

`36x^6y^3`

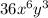
Explanation:

The problem needs application of law of indices

`1. (xy)^m = x^my^m`

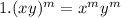
This means common power for terms can be applied to each term individually.

`x^a x^b = x^(a+b)\\`

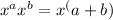
Separate power for the terms having same base can be added together.

_______________________________________________________

we will be using these law of indices in the problem

`(3xy)^2x^4y \\=> 3^2x^2y^2x^4y`

applied the first rule of indices as mentioned above

`3^2x^2y^2x^4y\\=>9*x^(2+4)4y^(2+1)\\=>9*4x^6y^3\\=>36x^6y^3`

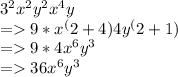
applied the second rule of indices as mentioned above

Thus, simplified form of (3xy)^2x^4y is
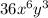`36x^6y^3`.