Question

The total cost (in dollars) for a company to manufacture and sell x items per week is C = 40 x + 640 , whereas the revenue brought in by selling all x items is R = 66 x − 0.2 x 2 . How many items must be sold to obtain a weekly profit of $ 200 ?

Answer 1

The company must sell 60 or 70 items to obtain a weekly profit of 200.

Explanation:

The profit is the difference between the revenue and the cost of a given task, therefore:

`\text{profit} = R - C\\\text{profit} = 66*x - 0.2*x^2 - (40*x + 640)\\\text{profit} = 66*x - 0.2*x^2 - 40*x - 640\\\text{profit} = - 0.2*x^2 + 26*x - 640`

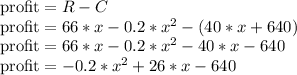
To have a profit of 200, we need to sell:

`-0.2*x^2 + 26*x - 640 = 200\\-0.2*x^2 + 26*x -840 = 0\text{ } *(-1)/(0.2)\\x^2 -130 + -4200 = 0\\x_(1,2) = (-(-130) \pm √((-130)^2 - 4*1*(-4200)))/(2*1)\\x_(1,2) = (130 \pm √(16900 + 16800))/(2)\\x_(1,2) = (130 \pm √(100))/(2)\\x_(1,2) = (130 \pm 10)/(2)\\x_(1) = (130 + 10)/(2) = (140)/(2) = 70\\ x_(2) = (130 - 10)/(2) = (120)/(2) = 60`

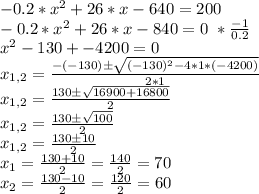
The company must sell 60 or 70 items to obtain a weekly profit of 200.