Question

The weights of college football players are normally distributed with a mean of 200 pounds and a standard deviation of 50 pounds. If a college football player is randomly selected find the probability that he weighs between 170 and 220 pounds.

Answer 1

The probability that he weighs between 170 and 220 pounds

P( 170 ≤ x≤ 200) = 0.3811

Step-by-step explanation:

Step-by-step explanation:-

Given mean of the Population = 200 pounds

Given standard deviation of the Population = 50 pounds

Let 'X' be the random variable of the weights of college football players are normally distributed.

Let x₁ = 170

`Z_(1) = (x_(1) - mean)/(S.D)`

`Z_(1) = (170 - 200)/(50)= -0.6`

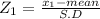
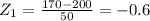
Let x₂ = 220

`Z_(2) = (x_(2) - mean)/(S.D)`

`Z_(2) = (220 - 200)/(50)= 0.4`

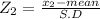
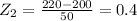
The probability that he weighs between 170 and 220 pounds.

P( 170 ≤ x≤ 200) = P(Z₁ ≤z≤Z₂)

= P(-0.6 ≤z≤0.4)

= P(z≤0.4)-P(z≤-0.6)

= 0.5 + A(0.4) -(0.5 - A(-0.6)

= A(0.4) + A(0.6) A(-z) = A(z)

= 0.1554 +0.2257 ( check Areas in normal table)

= 0.3811

Conclusion:-

The probability that he weighs between 170 and 220 pounds

P( 170 ≤ x≤ 200) = 0.3811