Answer:
The degrees of freedom are given by;
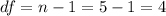
The significance level is 0.1 so then the critical value would be given by:
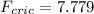
If the calculated value is higher than this value we can reject the null hypothesis that the arrivals are uniformly distributed over weekdays
Explanation:
For this case we have the following observed values:
Mon 25 Tue 22 Wed 19 Thu 18 Fri 16 Total 100
For this case the expected values for each day are assumed:
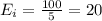
The statsitic would be given by:
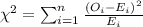
Where O represent the observed values and E the expected values
The degrees of freedom are given by;
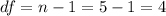
The significance level is 0.1 so then the critical value would be given by:
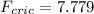
If the calculated value is higher than this value we can reject the null hypothesis that the arrivals are uniformly distributed over weekdays