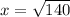Answer:
Explanation:
The geometric mean has a set up it must follow in order to "work". If you look at #3, x is a side of the smaller triangle that has a base of 3, but it's also a side of the large triangle that has a base of 3 + 8 which is 11. That means that x is your geometric mean. Setting up the geometric mean will look like this:
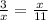
where x is the geometric means and the 3 and the 11 (the positions they are in) are the geometric extremes.
Now we cross multiply to solve for x:
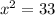 and
and
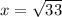
That's the length of x in #3.
For #4, x is the side of the small triangle with the base of 7 and it's also the side of the large triangle with the base of 7 + 13 which 20. That means that x is the geometric mean. Setting up like above:
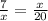 and
and
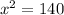 so
so