Answer:
Explanation:
Give the rate of change of sales revenue of a store modeled by the equation
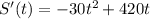 . The Total sales revenue function S(t) can be gotten by integrating the function given as shown;
. The Total sales revenue function S(t) can be gotten by integrating the function given as shown;
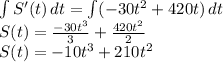
a) The total sales for the first week after the campaign ends (t = 0 to t = 7) is expressed as shown;
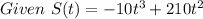
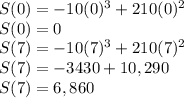
Total sales = S(7) - S(0)
= 6,860 - 0
Total sales for the first week = $6,860
b) The total sales for the secondweek after the campaign ends (t = 7 to t = 14) is expressed as shown;
Total sales for the second week = S(14)-S(7)
Given S(7) = 6,860
To get S(14);
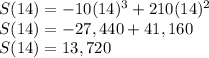
The total sales for the second week after campaign ends = 13,720 - 6,860
= $6,860